Анафем - Страница 284

К оглавлению

284

Дат разрезал.

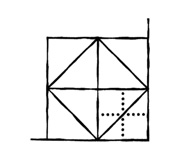
— Когда ты сделал первый диагональный разрез, ты разделил квадрат точно пополам, верно?

— Верно.

— И то же самое относится к трём другим диагональным разрезам и трём остальным квадратам?

— Конечно.

— Допустим, я повернул противень и ты посмотришь на него так:

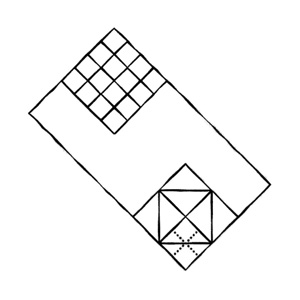
Какую фигуру ты видишь в середине?

— Квадрат.

— И сколько кусков коврижки в этом квадрате?

— Четыре.

— Он составлен из четырёх треугольников, верно?

— Ага.

— Каждый из треугольников — половина квадрата, верно?

— Верно.

— Сколько порций в маленьком квадрате?

— Четыре.

— Значит, в каждом треугольнике сколько порций?

— Две.

— А в квадрате, состоящем из четырёх таких треугольников?..

— Восемь порций. — Тут до него дошло: — Это та задача, которую мы пытались решить раньше!

— Мы всё время её решали, — поправил я. — Просто нам потребовалось несколько минут. А теперь отрежь нам, пожалуйста, восемь порций.

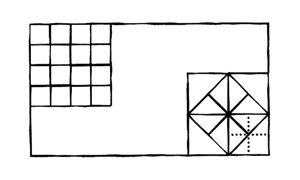
— Ну вот, — сказал я.

— А можно теперь есть?

— Конечно. Ты понял, что произошло?

— М-мм... Я отрезал восемь одинаковых порций коврижки?

— Ты так говоришь, будто это просто... но на самом деле мы проделали сложный путь, — сказал я. — Вспомни, несколько минут назад ты знал, как отрезать четыре порции. Знал, как отрезать шестнадцать. Девять — запросто. Но ты не знал, как отрезать восемь. Задача казалась неразрешимой. Однако мы хорошенько подумали и нашли ответ. И не приблизительный, а совершенно точный.

Кальк 2. Гемново (конфигурационное) пространство

Приложение к «Анафему» Нила Стивенсона

Так получилось, что, пока мы расхаживали туда-сюда, кто-то из нас задел ногой пустую винную бутылку, и она осталась лежать на кухонном полу вот так:

Пол был из дощечек, собранных в квадраты, что навело меня на мысль о координатной плоскости.

— Принеси доску и кусок мела, — сказал я Барбу.

Мне немножко стыдно было его так гонять, но я злился, что он мне не помог. Барб вроде бы не возражал и быстро выполнил просьбу, потому что доски и мел для записи рецептов и продуктов для готовки лежали по всей кухне.

— Теперь сделай мне одолжение: запиши на доске координаты бутылки.

— Координаты?

— Да. Считай рисунок пола лесперовой координатной сеткой. Давай договоримся, что сторона квадратика — единица. Я кладу картофелину сюда — это будет начало координат.

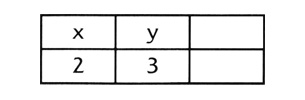
— Ну, тогда бутылка примерно на (2,3). — Барб некоторое время скрипел мелом, потом развернул доску ко мне.

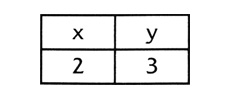
Вот, это уже конфигурационное пространство — почти самое простое, какое можно вообразить, — сказал я. — Положение бутылки — (2,3) — точка в этом пространстве.

— Тогда это просто обычное двумерное пространство, — возмутился Барб. — Почему ты так не говоришь?

— Можешь добавить ещё колонку?

— Конечно.

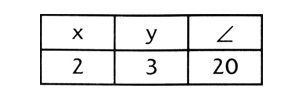
— Обрати внимание, что бутылка лежит не прямо. Она повёрнута примерно на одну десятую пи — или, в единицах, к которым ты привык в экстрамуросе, примерно на двадцать градусов. Угол поворота будет третьей координатой конфигурационного пространства — третьей колонкой в твоей таблице.

Барб взял мел и написал:

— Ладно, теперь это уже не просто скучное двумерное пространство, — признал он. — У него три измерения, и третье — необычное. Похоже на то, что нам объясняли в сувине...

— Полярные координаты? — спросил я, поражённый, что Барб про них знает. Видать, Кин потратил кучу денег, чтобы отправить его в хорошую сувину.

— Ага! Угол вместо расстояния.

— Давай посмотрим, как это пространство себя ведёт. Я буду двигать бутылку, а ты — отмечать её координаты всякий раз, как я скажу.

Я подвинул бутылку и немножко её повернул.

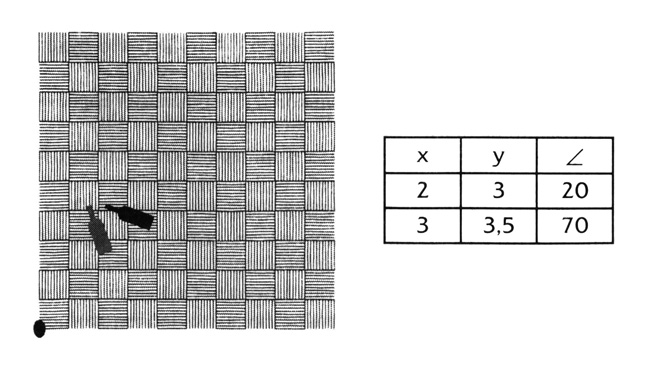
— Отмечай. Отмечай. Отмечай.

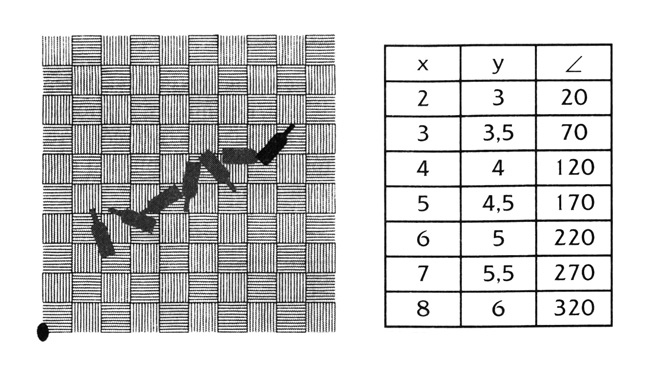
Я сказал:

— Видишь, множество точек в конфигурационном пространстве такое же, как если бы я нечаянно пнул бутылку, и она покатилась по полу. Согласен?

— Да. Я как раз сам так подумал!

— Но я двигал её медленно, чтобы тебе удобнее было записывать.

Барб не понял, как отвечать на мою убогую шутку. После неловкой паузы я продолжил:

— А можешь теперь составить график? Отметить эти точки на трёхмерном графике?

— Могу, — неуверенно протянул Барб. — Только это будет странно.

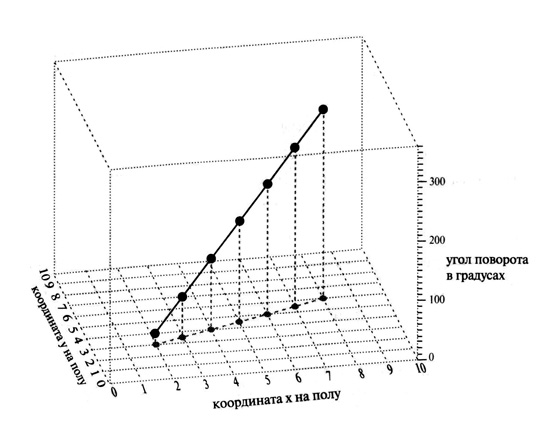
— Пунктир внизу показывает только x и y, — объяснил Барб. — Путь бутылки на полу.

— Хорошо, потому что пока ты не привык к конфигурационному пространству, остальное тебе будет непонятно, — сказал я. — Путь на плоскости xy, который ты показал пунктиром, вполне знаком нам по адрахонесову пространству — он просто показывает, как бутылка двигалась по полу. А вот третья координата — угол — совершенно другая история. Она показывает не буквальное расстояние в пространстве, а то, насколько повернулась бутылка. Как только ты это понял, ты можешь считать её прямо с графика и сказать: «Ага, бутылка лежала под углом двадцать градусов, а пока катилась по полу, повернулась ещё на триста». Но если ты не знаешь тайного шифра, ты ничего не поймёшь.

284